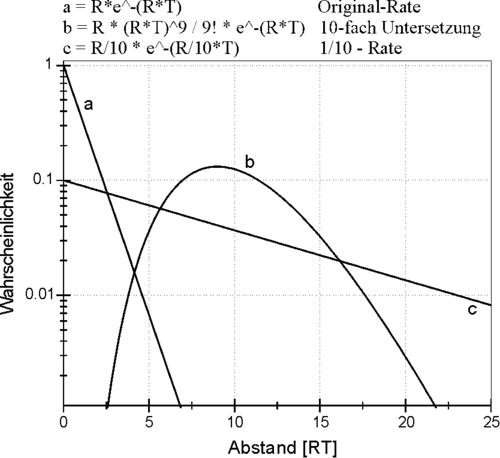
Abb. Abstandsverteilungen
[Inhalt]
(Totzeiten, Signalabstandsverteilungen)
März 1995 K. Huber, Strahlenzentrum Univ. Gießen
Version 22.Nov.2024
| • Rechnungen zur Poisson-Verteilung | ||
| • Anwendungen |
Nächste: Anwendungen, Nach oben: Top [Inhalt]
Bei den folgenden Betrachtungen wird davon ausgegangen, dass die Ereignisraten Poisson-verteilt sind.
| • Poisson-Verteilung | ||
| • Abstandsverteilungen für Poisson-verteilte Signale | ||
| • Totzeitverluste für Poisson-verteilte Signale |
Nächste: Abstand Poisson, Nach oben: Rechnungen zur Poisson-Verteilung [Inhalt]
Die Poisson-Verteilung wird in der folgenden Form benutzt:
Wahrscheinlichkeit P[n] für das Eintreffen von genau n Ereignissen im Zeitintervall [0,t]
P[n](R,t) = (R*t)^n / n! * e^-(R*t) t: Zeit > 0 R: Ereignisrate > 0 n: 0,1,...,~ Sum[n=0,~]P[n] = e^+(R*t) * e^-(R*t) = 1 Sum[n=0,~](n*P[n]) = R*t * Sum[n=0,~]P[n] = R*t P[n+1] = R*t / (n+1) * P[n] dP[n]/dt = R * (P[n-1] - P[n]) Int(P[n])dt = -1/R * Sum[i=0,n]P[i] Int[0,~]P[n]dt = 1/R
Nächste: Totzeitverluste, Vorige: Poisson-Verteilung, Nach oben: Rechnungen zur Poisson-Verteilung [Inhalt]
Die Änderung von P[0] zur Zeit t ist die Wahrscheinlichkeit für das Eintreffen des ersten Ereignisses seit t=0. Legt man t=0 auf den Zeitpunkt des vorausgegangenen Ereignisses, was man ohne Einschränkung tun kann, so erhält man die Wahrscheinlichkeit für das Auftreten des Abstandes t. P[0] wird um die Wahrscheinlichkeit kleiner, mit der das Ereingnis zur Zeit t eintrifft.
Die Änderung von P[1] enthält zwei Komponenten (s.o.): zum Einen muss es um den Anteil wachsen, den P[0] verloren hat, und zum Andern verliert es durch die Wahrscheinlichkeit des Eintreffens eines zweiten Ereignisses. Der zweite Anteil gibt uns die Abstandsverteilung des zweiten Ereignisses vom Startereignis.
dP[0]/dt = R * (0 - P[0])
dP[1]/dt = R * (P[0] - P[1])
...
dP[n]/dt = R * (P[n-1] - P[n])
Die Abstandsverteilung A[n] der n-ten Ereignisse nach einem Startereignis ist daher:
A[n] = R * P[n-1] Int[0,~](A[n])dt = 1
Von besonderem Interesse ist A[1], die Abstandsverteilung zwischen zwei benachbarten Ereignissen:
A[1] = R * P[0] = R * e^-(R*t)
Für Poisson-verteilte Signale ist es eine abfallende Exponentialfunktion, die, da sie in logarithmischer Darstellung eine Gerade ergibt, bequem zur Diagnose von experimentellen Störungen wie Totzeiten oder Nachimpulsen dienen kann.
Vorige: Abstand Poisson, Nach oben: Rechnungen zur Poisson-Verteilung [Inhalt]
Nächste: Abstand nicht paral, Nach oben: Totzeitverluste [Inhalt]
Ereignisse, die in eine Totzeit fallen, tragen selber nicht zur Totzeit bei.
R Eingangsrate vor der Totzeit
r Ausgangsrate nach der Totzeit
Td Totzeit
Vd = R*Td Totzeitverluste Vd im Totzeitintervall Td
bei Poisson-verteilter Eingangsrate R
Tt = r*t*Td gesamte Totzeit Tt in der Zeit t für die Ausgangsrate r
Rv = R*Tt/t Rate Rv der Totzeitverluste
R = r + Rv Bilanz der Raten
= r * (1 + R*Td)
R = r / (1 - r*Td) Totzeitkorrektur
r = R / (1 + R*Td) inverse Totzeitkorrektur
Die erste Gleichung ist nur für Poisson-verteilte Eingangsraten richtig. Bei periodischer Eingangsrate und R*Td < 1 würden keine Totzeitverluste auftreten.
Diese Gleichung ist auch direkt aus der Poisson-Verteilung herzuleiten:
V = 1*P[1] + 2*P[2] + ... + n*P[n] + ... = R*T*P[0] + R*T*P[1] + ... + R*T*P[n-1] + ... = R*T
Nächste: Korr paral, Vorige: Korr nicht paral, Nach oben: Totzeitverluste [Inhalt]
Nach den vorausgegangenen Überlegungen kann man den Zeitnullpunkt für die Abstandsmessung beliebig legen und erhält für Poisson-verteilte Ereignisse immer die gleiche Abstandsverteilung. Das erste nach einer vorausgegangenen Totzeit auftretende Ereignis hat deshalb von dem Totzeit auslösenden Ereignis die gewohnte Abstandsverteilung P[0] verschoben um die Totzeit T und vermindert um die Totzeitverluste in T.
A[1,T] = U(t-T) * r * P[0](t-T) = U(t-T) * R / (1 + R*T) * P[0](t-T) U(t) = 0 für t<0; 1 für t>=0; (Sprungfunktion)
Nächste: Abstand paral, Vorige: Abstand nicht paral, Nach oben: Totzeitverluste [Inhalt]
Ereignisse, die in eine Totzeit fallen, verlängern die Totzeit durch das Starten eines neuen Totzeitintervalls.
A = R * e^-(R*t) Abstandsverteilung der Ereignisse bei Eingangsrate R w = R * Int[T,~](e^-(R*t))dt = e^-(R*T) Wahrsch. w für Abstand größer Totzeit T r = R * e^-(R*T) gemessene Rate, max für R*T=1 R = ??? Totzeitkorrektur nur numerisch lösbar, oder für RT<<1 näherungsweise durch Reihenentwicklung
Nächste: Tab Totzeitverluste, Vorige: Korr paral, Nach oben: Totzeitverluste [Inhalt]
Diese Nuss ist noch zu knacken!
Vorige: Abstand paral, Nach oben: Totzeitverluste [Inhalt]
Tab.: rel. Totzeitverluste:
R*T !paralys paralys 0.00 0.000 0.000 0.10 0.091 0.095 0.20 0.167 0.181 0.30 0.231 0.259 0.40 0.286 0.330 0.50 0.333 0.393 0.60 0.375 0.451 0.80 0.444 0.551 1.00 0.500 0.632 1.50 0.600 0.777 2.00 0.667 0.865 2.50 0.714 0.918 3.00 0.750 0.950 4.00 0.800 0.982 5.00 0.833 0.993 6.00 0.857 0.998 8.00 0.889 1.000 10.00 0.909 1.000
Vorige: Rechnungen zur Poisson-Verteilung, Nach oben: Top [Inhalt]
Die folgenden Betrachtungen setzen stets eine feste, nicht-paralysierende Totzeit voraus!
| • Kaskadierte Zähler | ||
| • Vorgeschaltete Untersetzer | ||
| • Fifo-Speicher | ||
| • Dominierende Totzeit | ||
| • Beseitigen von Nachimpulsen | ||
| • Lifetime-Messung |
Nächste: Vorgeschaltete Untersetzer, Nach oben: Anwendungen [Inhalt]
Einige der (Eigenbau-) Datenerfassungsgeräte liefern über einen Ausgang einen Zählimpuls für jeden Totzeitverlust. Da ein nachgeschalteter Zähler jedoch ebenfalls eine Totzeit hat, gehen dort wiederum Ereignisse verloren, die man mit einem weiteren Zähler registrieren könnte usw.. Prinzipiell sollte jedoch aus den ersten beiden Raten die Originalrate berechenbar sein, falls die Totzeiten gleich sind und die Originalrate konstant ist.
Die Zählrate Z[0] und die Totzeitverluste V[0] der ersten Datenerfassung mit Totzeit T[0] sind
Z[0] = R/(1 + R*T[0])
V[0] = R - Z[0]
= R * R*T[0]/(1 + R*T[0])
Die zweite Datenerfassung erhält die gleiche primäre Datenrate R, jedoch um die V[0]/R verkürzte Zeit
Z[1] = R/(1 + R*T[1]) * V[0]/R
= R/(1 + R*T[1]) * R*T[0]/(1 + R*T[0])
V[1] = V[0] - Z[1]
= R * R*T[0]/(1 + R*T[0]) * R*T[1]/(1 + R*T[1])
usw...
Z[n] = R/(1 + R*T[n]) * V[n-1]/R
= 1/T[n] * Prod[i=0,n](R*T[i]/(1 + R*T[i]))
= Z[n-1] * T[n-1]/T[n] * R*T[n]/(1 + R*T[n])
V[n] = V[n-1] - Z[n]
= R - Sum[i=0,n]Z[i]
= R * Prod[i=0,n](R*T[i]/(1 + R*T[i]))
= V[n-1] * R*T[n]/(1 + R*T[n])
V[n]/Z[n] = R*T[n]
V[n]/R = Prod[i=0,n](R*T[i]/(1 + R*T[i]))
V[~] = 0
-> R = Sum[i=0,~]Z[i]
Für den Fall T[0]=T[1]=T genügen Z[0] und Z[1] zur Berechnung von V[1], R und T
R = Z[0]^2 / (Z[0] - Z[1])
= Z[0] + Z[1] * Sum[i=0,~]((Z[1]/Z[0])^i)
V[1] = Z[1]^2 / (Z[0] - Z[1])
T = Z[1] / Z[0]^2
Für den Fall T[0], T[1]=T[2]=T benötigt man Z[0], Z[1] und Z[2] zur Berechnung von R, V[2], T[0] und T
R = Z[0] + Z[1]^2 / (Z[1] - Z[2])
= Z[0] + Z[1] + Z[2] * Sum[i=0,~]((Z[2]/Z[1])^i)
V[2] = Z[2]^2 / (Z[1] - Z[2])
T[0] = Z[1]^2 / (Z[0]^2 * (Z[1] - Z[2]) + Z[0]*Z[1]^2)
T = Z[2] / (Z[0] * (Z[1] - Z[2]) + Z[1]^2)
Nächste: Fifo-Speicher, Vorige: Kaskadierte Zaehler, Nach oben: Anwendungen [Inhalt]
Bei zu hohen Zählraten ist zur Vermeidung von Totzeitverlusten die Vorschaltung eines schnellen Untersetzers zu empfehlen (z.B. 1/10, 50MHz). Dies hat zum einen den Effekt, dass die zu übertragende Rate reduziert wird und zum anderen, dass die statistischen Schwankungen der Zählrate herabgesetzt werden, wodurch sich ebenfalls die Totzeitverluste reduzieren.
R Originalrate, Poisson-verteilt Ru untersetzte Rate U >1 Untersetzungsverhältnis S <U systematischer Fehler durch Untersetzung F(R) statistischer Fehler von R R= U * Ru + S F(R)= SQRT(R)= SQRT(U*Ru+S) F(Ru)= F(R)/U= SQRT(U*Ru+S)/U= SQRT(Ru+S/U) / SQRT(U) für S<<R und 1<<Ru: F(Ru)~~ SQRT(Ru/U)
Bei der Auswertung ist zu beachten, dass der statistische Fehler nicht mehr wie gewohnt durch SQRT(Ru) gegeben ist. Additiv hinzu kommt ein systematischer Fehler S < U, der daher rührt, dass der Untersetzer jeweils U Ereignisse sammeln muss bevor ein Übertrag erscheint.
| • Verteilung der untersetzten Datenrate | ||
| • Totzeitverlustrechnung für die untersetzte Datenrate | ||
| • Abstandsverteilung der untersetzten Datenrate |
Nächste: Totzeitverlustrechnung, Nach oben: Vorgeschaltete Untersetzer [Inhalt]
Nach Durchlaufen eines 1/u - Untersetzters geht die Datenrate R in eine Rate Ru = R/u über, die keine Poisson-Verteilung mehr hat. Da jeweils erst nach u Eingangsereignissen ein Ereignis am Ausgang erscheint, ist die Wahrscheinlichkeit für das Auftreten von n Ereignissen am Ausgang bis zur Zeit t
U[n] = P[m] = (R*t)^m / m! * e^-(R*t) mit m = u * n
Nächste: Abstandsverteilung, Vorige: Verteilung, Nach oben: Vorgeschaltete Untersetzer [Inhalt]
In einer dem Untersetzer nachfolgenden nicht-paralysierenden Totzeit T gehen
V(u,R) = Sum[n=1,~](n * U[n])
= Sum[n=1,~](n * (R*T)^m / m! * e^-(R*T))
Ereignisse verloren.
speziell:
V(u=1,R) = Sum[n=1,~](n * P[n])
= Sum[n=1,~](R*T * P[n-1])
= (R*T) * Sum[n=0,~](P[n])
= (R*T)
V(u=1,R/u) = (R*T)/u
Da für
V(u,R) = (R*T)/u * Sum[n=1,~]((R*T)^(m-1) / (m-1)! * e^-(R*T))
nur die höheren Glieder m = u-1, 2u-1,... der e^(R*T) Reihe einen Beitrag leisten, beschränken wir uns für (R*T)<1 und u>4 auf den Term n=1:
V(u,R,n=1) = (R*T)/u * (R*T)^(u-1) / (u-1)! * e^-(R*T))
= (R*T) * (R*T)^(u-1) / u! * e^-(R*T))
Die Totzeitverluste werden im Vergleich zur Eingangsrate R um mehr als 1/u! reduziert und werden z.B. bei einer 1/10-Untersetzung (1/10! = 2.8*10^-7) völlig venachlässigbar. Im Vergleich zu einer Eingangsrate R/u werden sie um mehr als 1/(u-1)! reduziert.
Vorige: Totzeitverlustrechnung, Nach oben: Vorgeschaltete Untersetzer [Inhalt]
Bei einem u-fachen Untersetzer ist die Wahrscheinlichkeit für das Eintreffen des u-ten Ereignisses von Interesse, da nur jedes u-te Ereignis am Ausgang erscheint. Wie oben gezeigt ist die Abstandsverteilung A[u] der u-ten Ereignisse bei der Eingangsrate R:
A[u] = R * P[u-1]
Mittelwerte von A[u]:
M(A[u]) = Int[0,~](t * A[u])dt / Int[0,~](A[u])dt
= u/R * Int[0,~](A[u]+1)dt
= u/R (war ja zu erwarten)
M(A[u]^2) = Int[0,~](t^2 * A[u])dt / Int[0,~](A[u])dt
= u * (u + 1) / R^2 * Int[0,~](A[u]+2)dt
= u * (u + 1) / R^2
Streuung um den Mittelwert:
S[u](R) = (A[u] - [M(A[u]))^2 = M(A[u]^2) - M(A[u])^2 = u / R^2
Die Streuung einer Poisson-verteilten gleichen Rate R/u hingegen ist
S[1](R/u) = u^2 / R^2,
also das u-fache. Die "statistischen Spitzen" werden geglättet.

Abb. Abstandsverteilungen
Nächste: Dominierende Totzeit (PDT), Vorige: Vorgeschaltete Untersetzer, Nach oben: Anwendungen [Inhalt]
Sobald ganze Datenworte mit einem Ereignis verbunden sind können vorgeschaltete Untersetzer oder Zählerkaskaden nicht benutzt werden zur Vermeidung von Totzeitverlusten. Hier können dann Fifo-Speicher weiterhelfen.
Dies ist der nicht ganz überzeugende Versuch das Problem als Markov-System bzw. Markov-Kette zu betrachten. Aber die Ergebnisse scheinen zu stimmen.(?)
Markov-Ketten-Modell für einen Fifo:
.--> /----\ -----l----> /----\ -----l----> /----\ ---. m |S(0)| |S(1)| |S(M)| l `--- \----/ <----m----- \----/ <----m----- \----/ <--' S(n): Besetzungswahrscheinlichkeit für Zustand mit n Ereignissen im Fifo S(0): Fifo ist leer S(m): Fifo ist voll l,m: Übergangswahrscheinlichkeiten l: Einströmung m: Bedienung
Ein Zustand S(n) wird zerstört mit der Wahrscheinlichkeit
(l + m) * S(n)
Und er wird aus den Nachbarn erzeugt mit der Wahrscheinlichkeit
m * S(0) + m * S(1) (n=0) l * S(n-1) + m * S(n+1) l * S(M-1) + l * S(M) (n=M)
Das System ist im Gleichgewicht, wenn beide Wahrscheinlichkeiten gleich sind
l * S(0) = m * S(1) (l + m) * S(n) = l * S(n-1) + m * S(n+1) m * S(M) = l * S(M-1)
Durch rekursives Einsetzen erhält man für die Besetzungswahrscheinlichkeiten S(n)
S(1) = (l/m)^1 * S(0) S(2) = (l/m)^2 * S(0) ... S(n) = (l/m)^n * S(0)
Für einen Fifo der Tiefe M gilt außerdem
Sum[n=0,M]S(n) = 1 = Sum[n=0,M]<(l/m)^n * S(0)>
S(0) = 1 / Sum[n=0,M]<(l/m)^n>
= (1 - l/m) / (1 - (l/m)^(M+1)) l/m != 1
= 1 / (M + 1) l/m = 1
und damit
S(n) = (l/m)^n * (1 - l/m) / (1 - (l/m)^(M+1)) l/m != 1
= 1 / (M + 1) l/m = 1
Die Wahrscheinlichkeit, dass der Fifo belegt ist, ergibt sich dann zu
S(M) = (l/m)^M * (1 - l/m) / (1 - (l/m)^(M+1)) l/m != 1
= 1 / (M + 1) l/m = 1
und die Rate der Verluste zu
V = S(M) * l
Für l/m << 1 kann man abschätzen
S(M) ~ (l/m)^M
Bleibt noch die Frage, wie die Übergangswahrscheinlichkeiten l und m zu verstehen sind. Setzt man
l = R Ereignisrate m = 1/T Bedienung mit Totzeit T (Bedienrate)
so erhält man einleuchtende Ergebnisse für einige überprüfbare Fälle (M=1, M=~, R*T<<1, R*T=1), obwohl dies nicht den Markov-Vorausetztungen (zufällige Ereignisse, die Vergangenheit hat keinen Einfluss) entspricht. Insbesondere ist die Bedienung eine direkte Folge eines vorausgegangenen Ereignisses und nicht zufällig.
Die Übergangswahrscheinlichkeit l kann man sich aus der Poisson-Verteilung der Ereignisrate als Wahrscheinlichkeit für das Auftreten des ersten Ereignisses "gleich jetzt" (t=0) folgendermaßen ableiten:
d(P[1]) / dt [t=0] = R d(P[n>1]) / dt [t=0] = 0
Für die Bedienrate mit Totzeit T geht das so nicht. Es gibt Rechnungen mit "negativ exponentieller" Bedienrate. Da soll das analog funktionieren:
B = 1 - e^-(t/T) (???) d(B) / dt [t=0] = 1/T
Haben wir aber nicht!
Wenn sowohl Ereignisrate als auch Bedienrate periodisch wären, so hätte man für R*T<1 garkeine Totzeitverluste zu erwarten. Mit einer zufälligen Ereignisrate scheint es aber noch zu funktionieren. Der Unterschied ist in der Formel für die Totzeitverluste
V = R * S(M)
zu berücksichtigen, die so nur richtig ist für eine zufällige Ereignisrate. Bei periodischen Ereignissen mit R*T<1 wäre die vorausgegangene Bedienung bereits beendet, wenn das nächste Ereignis eintrifft. Zufällige Ereignisse scheinen die Vergangenheit ausreichend abzukoppeln.
Beispiel:
Für ein Gerät mit Totzeit T und einem Datenregister
(M = 1) sind die Totzeitverluste bei einer Rate R
V = R * S(M) = R*R*T / (1 + R*T)
Das gleiche Ergebnis erhält man mit der üblichen Totzeitrechnung (s.o.).
Ergebnis:
Ein Fifo kann die Totzeitverluste erheblich vermindern.
V ~ R * (R/T)^M R*T << 1 V = R / (M + 1) R*T = 1
Für R*T << 1 genügt bereits ein Fifo mit wenigen
Speicherplätzen.
Für R*T = 1 können die Verluste
mit einem M = 100 Fifo auf 1% begrenzt werden.
Das Fifo auf der Rechneranpassung ist mit M = 2048 deutlich größer gewählt, da es mögliche Unterbrechungen bei der Datenverarbeitung durch den Rechner überbrücken muss:
z.B.: M / R = 2000 / 100kHz = 20ms
Nächste: Beseitigen von Nachimpulsen, Vorige: Fifo-Speicher, Nach oben: Anwendungen [Inhalt]
Gelegentlich sind Totzeiverluste nicht berechenbar da z.B. die Totzeit nicht bekannt oder veränderlich ist. In einem solchen Fall kann mit der "Programmierbaren Totzeit" eine Totzeit erzeugt werden, die die vorausgehenden, unbekannten Totzeiten dominiert.
Hier soll untersucht werden, inwiefern eine dominierende Totzeit geeignet ist, unbekannte Totzeiten so zu überdecken, dass Totzeitkorrekturrechnungen möglich werden.
Wie die folgenden Überlegungen zeigen, kann eine solche dominierende Totzeit nur näherungsweise funktionieren. Die Rechnungen zeigen zeigen in welcher Größenordnung Abweichungen zu erwarten sind und wie man sie eventuell minimieren kann.
Wie Simulationen gezeigt haben, sind die Abweichungen für eine nicht-paralysierende dominierende Totzeit deutlich kleiner als für eine paralysierende.
Nicht-paralysierende dominierende Totzeit
Die primäre Totzeit wird ebenfalls als nicht-paralysierend
und konstant vorausgesetzt.
Für nicht-paralysierende Totzeiten ergibt sich folgendes Verhalten:
E0 E1 E2 E3 En __|____|_____|______|____ T0 __|^^^^^^^^|_____________ Td __|^^^^^^^^^^^^^^^|______ T2 _____________|^^^^^^^^|__ Te __|^^^^^^^^^^^^^^^^^^^|__
Die Totzeitverluste können daher größer sein als die dominierende Totzeit erwarten lässt. Für T0=0 oder Td=T0 ist die Totzeitverlustrechnung Td exakt.
Rechnung
R: Eingangsrate vor allen Totzeiten r: Ausgangsrate nach den Totzeiten r': Ausgangsrate bei T0 = 0 Tp: primäre Totzeit Td: dominierende Totzeit (nicht-paralysierend Vd=R*Td) Vp: zusätzliche Totzeitverluste durch Tp bei Tp < Td Vd: Totzeitverluste durch Td bei Tp = 0
E0 E1 E2 E3 En __|____|_____|______|__________ Tp __|^^^^^^^^^^^|________________ Td __|^^^^^^^^^^^^^^^|____________ Tx ______________|^^^|____________ Tp ________________|^^^^^^^^^^^|__ Ty __________________|^^^^^^^^^|__
Tx = Td - Tp Ty = Tp - Tx/2 Vy = R*Ty * R*Tx = R^2 * (Td-Tp) * (3Tp-Td)/2 für Td = Tp --> Vy = 0 für Td = 2Tp --> Vy = 1/2 * (R*Tp)^2
Paralysierende dominierende Totzeit
Für eine nicht-paralysierende primäre Totzeit und eine
paralysierende dominierende Totzeit ergibt sich folgendes Verhalten:
E0 E1 E2 E3 En __|____|_____|______|___________ T0 __|^^^^^^^^|____________________ Td __|^^^^^^^^^^|^^^^^^^^^^^^^^^|__ T2 _____________|^^^^^^^^|_________ Te __|^^^^^^^^^^^^^^^^^^^^^^^^^^|__
Durch die primären Verluste von E1 und E3 wird die effektive Totzeit Td zu kurz. Für T0->0 verschwindet dieser Verlust.
Rechnung
R: Eingangsrate vor allen Totzeiten r: Ausgangsrate nach den Totzeiten r': Ausgangsrate bei T0 = 0 Tp: primäre Totzeit Td: dominierende Totzeit (nicht-paralysierend Vd=R*Td) Vp: zusätzliche Totzeitverluste durch Tp bei Tp < Td Vd: Totzeitverluste durch Td bei Tp = 0
Rechnung schwierig, noch ungelöst....
Simulationsrechnungen
Die folgenden Grafiken sind Ergebnisse von Monte-Carlo-Simulationen,
da für echte Messungen keine ausreichend gute Poisson-verteilte
Ereignisraten zur Verfügung standen. Der Versuch das Ganze mittels
Faltungsintegralen zu berechnen ist ebenfalls an der Komplexität
der Probleme gescheitert.
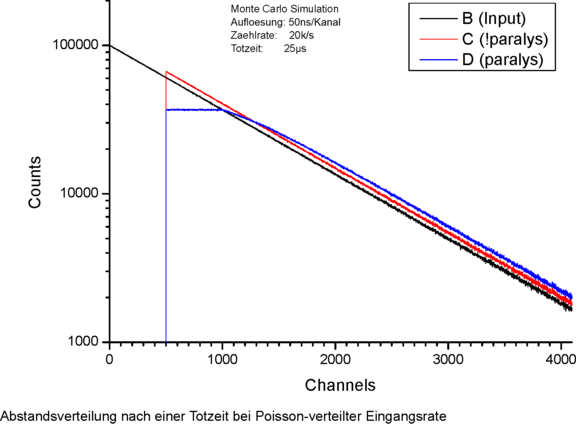
Sie zeigen die Abstandsverteilungen von Poisson-verteilten Ereignissen nach Durchlaufen von ein bzw. zwei Totzeiten. Wie man sieht haben Totzeiten einen markanten Einfluss auf die Abstandsverteilung und sind nicht nur ein Abschneiden von kurzen Abständen.
Die Abstandsverteilung von Poisson-verteilten Ereignissen ist eine abfallende Exponentialfunktion, in logarithmischer Darstellung also eine Gerade. Eine solche Verteilung lässt sich aus Zufallszahlen leicht herstellen, sodass eine Monte-Carlo-Rechnung ein bequemes Werkzeug zur Untersuchung der Auswirkungen einer Totzeit bei den verschiedenen Anwendungen ist.
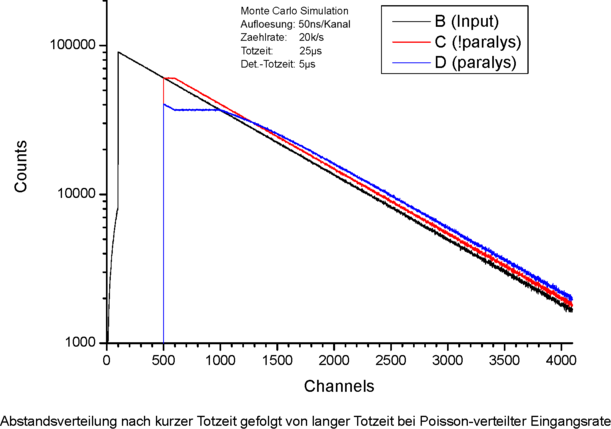
wie zuvor, Ausschnitt
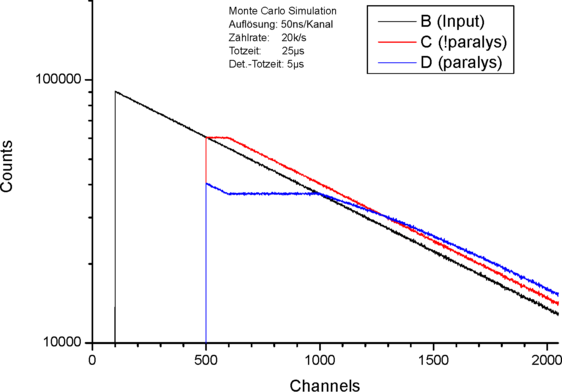
Nächste: Lifetime-Messung, Vorige: Dominierende Totzeit (PDT), Nach oben: Anwendungen [Inhalt]
Insbesondere Channeltrons haben die unschöne Eigenschaft nach einem echten Ereignis noch Nachimpulse zu liefern, die eine Wirkungsquerschnittmessung deutlich verfälschen können.
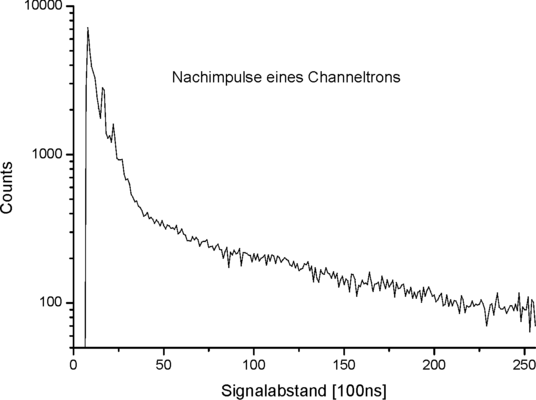
Totzeit (500ns) und Nachimpulse (bis ca. 4 us) eines Channeltrons
In dieser logarithmischen Darstellung der Ereignisabstände ist eine
markannte Abweichung von der zu erwartenden Geraden durch die
Poisson-verteilten Ereignisse zu erkennen. Mit einer geeigneten Totzeit
kann der Bereich der Nachimpulse ausgeblendet werden.
Wie man sich leicht überlegen kann, ist die nicht-paralysierende Totzeit
nicht dazu geeignet, da nach wie vor beliebig kurze Ereignisabstände
auftreten können.
Die paralysierende Totzeit hingegen entfernt alle Ereignisse, die zu ihrem
Vorgänger einen kürzeren Abstand haben als die Totzeit. Allerdings mit
Nebenwirkungen, s.o.
Siehe auch:
http://www.strz.uni-giessen.de/ExpHelp/datarout/datarout.html
http://www.strz.uni-giessen.de/ExpHelp/datarout/datarout.pdf
Vorige: Beseitigen von Nachimpulsen, Nach oben: Anwendungen [Inhalt]
Bei unbekannter bzw. variabler Totzeit eines Datenerfassungsgerätes oder wechselnder Ereignisrate ist es i.a. nicht möglich im Nachhinein eine Totzeitkorrekturrechnung durchzuführen. Deshalb bietet das Data-Routing zwei Möglichkeiten zur direkten Messung von Totzeiten an.
Lifetime-Messung mit der IFS-Karte
Lifetime-Messung mit der Zähler/Uhr-Karte